欢迎来到我的主页!
0%

LeetCode第一百零五题：从前序与中序遍历序列构造二叉树

发表于 更新于 分类于
本文字数： 2k 阅读时长 ≈ 2 分钟

引言：本文主要介绍LeetCode第一百零五题，给定一个二叉树的前序遍历和中序遍历结果，构造出二叉树，并给出c++实现。

题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例1

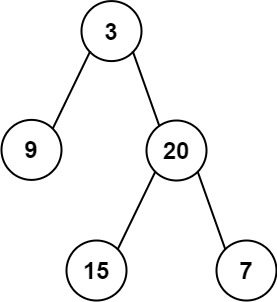
image.png

1
2
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例2

1
2
输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder 和 inorder 均 无重复 元素
  • inorder 均出现在 preorder
  • preorder 保证 为二叉树的前序遍历序列
  • inorder 保证 为二叉树的中序遍历序列

分析

对于任意一颗树而言，前序遍历的形式总是

1
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

1
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要 O(1)O(1) 的时间对根节点进行定位了。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    std::unordered_map<int, int> hashmap;
    TreeNode* buildTHelper(const std::vector<int>& preorder,
                              int pre_start_idx,
                              const std::vector<int>& inorder,
                              int in_start_idx,
                              int size) {
        TreeNode* node = new TreeNode();
        node->val = preorder[pre_start_idx];
        // 左子树存在
        int left_size = hashmap[node->val] - in_start_idx;
        if (left_size > 0) {
            node->left = buildTHelper(preorder,
                                         pre_start_idx + 1,
                                         inorder,
                                         in_start_idx,
                                         left_size);
        } else {
            node->left = nullptr;
        }
        // 右子树存在
        int right_size = size - 1 - left_size;
        if (right_size > 0) {
            node->right = buildTHelper(preorder,
                                          pre_start_idx + 1 + left_size,
                                          inorder,
                                          in_start_idx + 1 + left_size,
                                          right_size);
        } else {
            node->right = nullptr;
        }
        return node;
                                  
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        for (size_t i = 0; i < inorder.size(); ++i) {
            hashmap[inorder[i]] = i;
        }
        return buildTHelper(preorder,
                               0,
                               inorder,
                               0,
                               inorder.size());
    }
};

拓展

本题还有迭代实现方法，比较巧妙，有兴趣可以看看。