引言:本文主要介绍LeetCode第九十六题,不同的二叉搜索树数量,并给出c++实现。
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树有多少种?返回满足题意的二叉搜索树的种数。
示例1
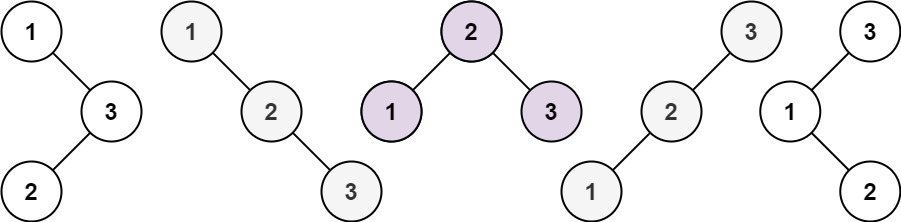
1 | 输入:n = 3 |
示例2
1 | 输入:n = 1 |
提示:
- 1 <= n <= 19
分析
这道题首先要搞清楚二叉搜索树的定义,二叉搜索树的左儿子一定比根结点小,右儿子一定比根结点大,而且所有子树也一定是二叉搜索树。这道题其实和结点的值无关,只与大小关系有关,我们以从1到n的结点分别做为根结点,那么每种情况就是比根结点小的结点都在左子树上,大的都在右子树上,而子树的情况,也是这样,当以i为根结点时,那么左子树的情况就是G(i-1),右子树的情况就是G(n - 1 - i),所以G(i - 1) * G(n - 1 - i)就是以i为根结点的所有情况数量,以其他结点为根结点时也是类似,所以加在一起有如下递推关系式:
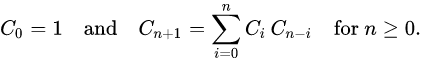
实现
1 | int numTrees(int n) { |
拓展
其实满足上述递推关系式的数叫做卡塔兰数,可以证明,卡塔兰数的递推关系式如下:
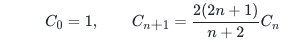
推导如下。