欢迎来到我的主页!
0%

Leetcode第九十四题：二叉树的中序遍历

发表于 更新于 分类于
本文字数： 1.1k 阅读时长 ≈ 1 分钟

引言：本文主要介绍LeetCode第九十四题，对二叉树进行中序遍历，并给出c++实现。

题目

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例1

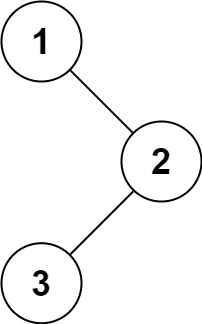
image.png

1
2
输入：root = [1,null,2,3]
输出：[1,3,2]

示例2

1
2
输入：root = []
输出：[]

示例3

1
2
输入：root = [1]
输出：[1]

示例4

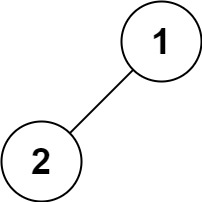
image.png

1
2
输入：root = [1,2]
输出：[2,1]

示例5

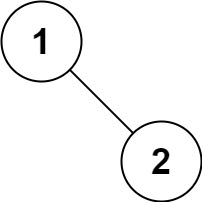
image.png

1
2
输入：root = [1,null,2]
输出：[1,2]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

分析

中序遍历先访问左儿子，最后访问右儿子，对于子树也是如此。递归方法很容易想到，代码也很简单；迭代的话就是自己维护一个stack，先将根结点入栈，然后将左儿子入栈，再将左儿子的左儿子入栈，如此，直到没有左儿子，然后将栈顶结点出栈，将其值加入结果，然后对其右儿子执行上述操作，直到栈为空且所有结点都遍历过。

代码

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void inorder(TreeNode* root, vector<int>& res) {
    if (!root) {
        return;
    }
    inorder(root->left, res);
    res.emplace_back(root->val);
    inorder(root->right, res);
}

vector<int> inorderTraversal(TreeNode* root) {
    std::vector<int> res;
    inorder(root, res);
    return res;
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> inorderTraversal(TreeNode* root) {
    std::vector<int> res;
    std::stack<TreeNode*> stack;
    while (root || !stack.empty()) {
        while (root) {
            stack.push(root);
            root = root->left;
        }
        if (!root) {
            root = stack.top()
            stack.pop();
            res.emplace_back(root->val);
            root = root->right;
        }
    }
}

拓展

以上两种方法时间复杂度和空间复杂度都是O(n)，还有一种空间复杂度为O(1)的方法，Morris方法，之后再讨论。