欢迎来到我的主页!
0%

数据结构及实现：AVL树

发表于 更新于 分类于
本文字数： 26k 阅读时长 ≈ 24 分钟

引言：对AVL树的理论知识进行简单介绍，给出C++实现，并对实现代码进行了测试。

AVL树简介

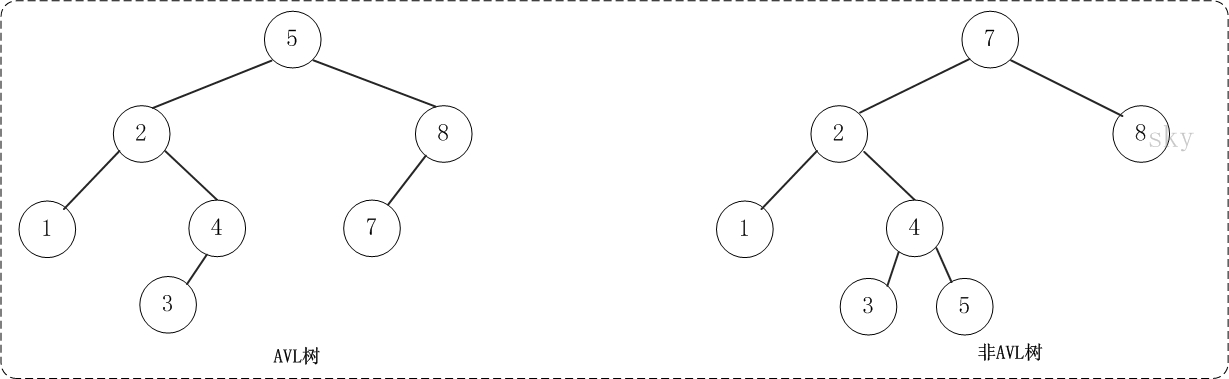
AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的。它是最先发明的自平衡二叉查找树，也被称为高度平衡树。相比于"二叉查找树"，它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。

AVL树和非AVL.jpg

上面的两张图片，左边的是AVL树，它的任何节点的两个子树的高度差别都<=1；而右边的不是AVL树，因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3，而以8为根节点的树的高度是1)。

AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。如果在AVL树中插入或删除节点后，使得高度之差大于1。此时，AVL树的平衡状态就被破坏，它就不再是一棵二叉树；为了让它重新维持在一个平衡状态，就需要对其进行旋转处理。学AVL树，重点的地方也就是它的旋转算法；在下文的介绍中，来对它进行详细介绍。

AVL树的C++实现

节点

AVL树节点
1
2
3
4
5
6
7
8
9
10
11
template <class T>
class AVLTreeNode {
public:
    T key;                // 关键字(键值)
    int height;         // 高度
    AVLTreeNode *left;    // 左孩子
    AVLTreeNode *right;    // 右孩子

    AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
    	key(value), height(0),left(l),right(r) {}
};

AVLTreeNode是AVL树的节点类，它包括的几个组成对象:
（1） key – 是关键字，是用来对AVL树的节点进行排序的。
（2） left – 是左孩子。
（3） right – 是右孩子。
（4） height – 是高度。

AVL树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
template <class T>
class AVLTree {
private:
    AVLTreeNode<T> *mRoot;    // 根结点

public:
    AVLTree();
    ~AVLTree();

    // 获取树的高度
    int height();
    
    // 获取树的高度
    int max(int a, int b);

    // 前序遍历"AVL树"
    void preOrder();
    
    // 中序遍历"AVL树"
    void inOrder();
    
    // 后序遍历"AVL树"
    void postOrder();

    // (递归实现)查找"AVL树"中键值为key的节点
    AVLTreeNode<T>* search(T key);
    
    // (非递归实现)查找"AVL树"中键值为key的节点
    AVLTreeNode<T>* iterativeSearch(T key);

    // 查找最小结点：返回最小结点的键值。
    T minimum();
    
    // 查找最大结点：返回最大结点的键值。
    T maximum();

    // 将结点(key为节点键值)插入到AVL树中
    void insert(T key);

    // 删除结点(key为节点键值)
    void remove(T key);

    // 销毁AVL树
    void destroy();

    // 打印AVL树
    void print();
    
private:
    // 获取树的高度
    int height(AVLTreeNode<T>* tree) ;

    // 前序遍历"AVL树"
    void preOrder(AVLTreeNode<T>* tree) const;
    
    // 中序遍历"AVL树"
    void inOrder(AVLTreeNode<T>* tree) const;
    
    // 后序遍历"AVL树"
    void postOrder(AVLTreeNode<T>* tree) const;

    // (递归实现)查找"AVL树x"中键值为key的节点
    AVLTreeNode<T>* search(AVLTreeNode<T>* x, T key) const;
    
    // (非递归实现)查找"AVL树x"中键值为key的节点
    AVLTreeNode<T>* iterativeSearch(AVLTreeNode<T>* x, T key) const;

    // 查找最小结点：返回tree为根结点的AVL树的最小结点。
    AVLTreeNode<T>* minimum(AVLTreeNode<T>* tree);
    
    // 查找最大结点：返回tree为根结点的AVL树的最大结点。
    AVLTreeNode<T>* maximum(AVLTreeNode<T>* tree);

    // LL：左左对应的情况(左单旋转)。
    AVLTreeNode<T>* leftLeftRotation(AVLTreeNode<T>* k2);

    // RR：右右对应的情况(右单旋转)。
    AVLTreeNode<T>* rightRightRotation(AVLTreeNode<T>* k1);

    // LR：左右对应的情况(左双旋转)。
    AVLTreeNode<T>* leftRightRotation(AVLTreeNode<T>* k3);

    // RL：右左对应的情况(右双旋转)。
    AVLTreeNode<T>* rightLeftRotation(AVLTreeNode<T>* k1);

    // 将结点(z)插入到AVL树(tree)中
    AVLTreeNode<T>* insert(AVLTreeNode<T>* &tree, T key);

    // 删除AVL树(tree)中的结点(z)，并返回被删除的结点
    AVLTreeNode<T>* remove(AVLTreeNode<T>* &tree, AVLTreeNode<T>* z);

    // 销毁AVL树
    void destroy(AVLTreeNode<T>* &tree);

    // 打印AVL树
    void print(AVLTreeNode<T>* tree, T key, int direction);
};

AVLTree是AVL树对应的类。它包含AVL树的根节点mRoot和AVL树的基本操作接口。需要说明的是：AVLTree中重载了许多函数。重载的目的是区分内部接口和外部接口，例如insert()函数而言，insert(tree, key)是内部接口，而insert(key)是外部接口。

树的高度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*
 * 获取树的高度
 */
template <class T>
int AVLTree<T>::height(AVLTreeNode<T>* tree) {
    if (tree != NULL)
        return tree->height;

    return 0;
}

template <class T>
int AVLTree<T>::height() {
    return height(mRoot);
}

关于高度，有的地方将"空二叉树的高度是-1"，而本文采用维基百科上的定义：树的高度为最大层次。即空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)。

比较大小
1
2
3
4
5
6
7
/*
 * 比较两个值的大小
 */
template <class T>
int AVLTree<T>::max(int a, int b) {
    return a>b ? a : b;
}

旋转

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

AVL树旋转.jpg

上图中的4棵树都是"失去平衡的AVL树"，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL树，如下图：

AVL树旋转2.jpg

上面的两张图都是为了便于理解，而列举的关于"失去平衡的AVL树"的例子。总的来说，AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一，它们都由各自的定义：

（1）LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

（2）LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

（3）RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

（4）RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。例如，在上面RR情况中，由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

前面说过，如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍"LL(左左)，LR(左右)，RR(右右)和RL(右左)"这4种情况对应的旋转方法。

LL的旋转

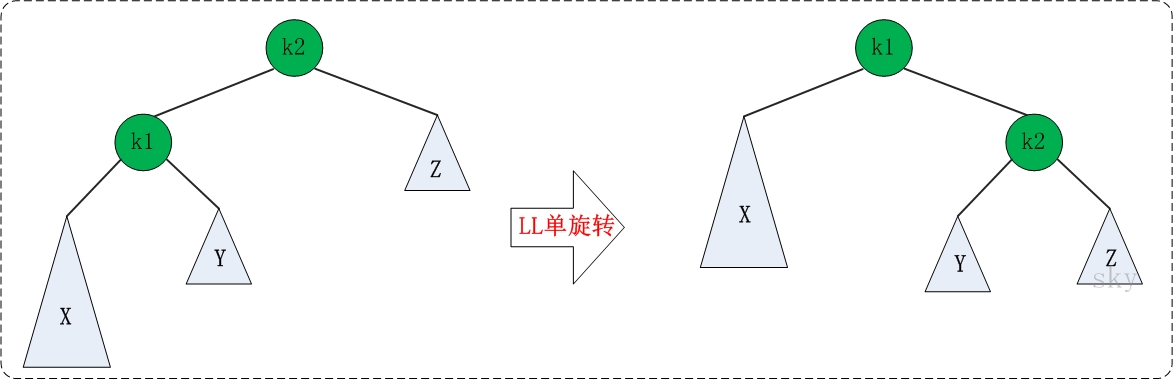
LL失去平衡的情况，可以通过一次旋转让AVL树恢复平衡。如下图：

LL旋转.jpg

图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了AVL树，而且该旋转只需要一次即可完成。对于LL旋转，你可以这样理解为：LL旋转是围绕"失去平衡的AVL根节点"进行的，也就是节点k2；而且由于是LL情况，即左左情况，就用手抓着"左孩子，即k1"使劲摇。将k1变成根节点，k2变成k1的右子树，“k1的右子树"变成"k2的左子树”。

LL的旋转代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::leftLeftRotation(AVLTreeNode<T>* k2) {
    AVLTreeNode<T>* k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = max( height(k2->left), height(k2->right)) + 1;
    k1->height = max( height(k1->left), k2->height) + 1;

    return k1;
}
RR的旋转

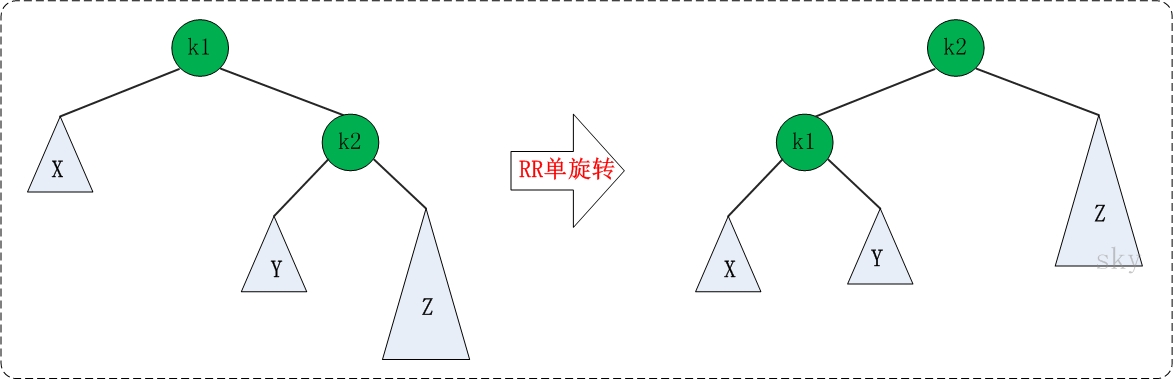
理解了LL之后，RR就相当容易理解了。RR是与LL对称的情况！RR恢复平衡的旋转方法如下：

RR旋转.jpg

图中左边是旋转之前的树，右边是旋转之后的树。RR旋转也只需要一次即可完成。

RR的旋转代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::rightRightRotation(AVLTreeNode<T>* k1) {
    AVLTreeNode<T>* k2;

    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = max( height(k1->left), height(k1->right)) + 1;
    k2->height = max( height(k2->right), k1->height) + 1;

    return k2;
}
LR的旋转

LR失去平衡的情况，需要经过两次旋转才能让AVL树恢复平衡。如下图：

LR旋转.jpg

第一次旋转是围绕"k1"进行的"RR旋转"，第二次是围绕"k3"进行的"LL旋转"。

LR的旋转代码

1
2
3
4
5
6
7
8
9
10
11
/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::leftRightRotation(AVLTreeNode<T>* k3) {
    k3->left = rightRightRotation(k3->left);

    return leftLeftRotation(k3);
}
RL的旋转

RL是与LR的对称情况！RL恢复平衡的旋转方法如下：

RL旋转.jpg

第一次旋转是围绕"k3"进行的"LL旋转"，第二次是围绕"k1"进行的"RR旋转"。

RL的旋转代码

1
2
3
4
5
6
7
8
9
10
11
/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::rightLeftRotation(AVLTreeNode<T>* k1) {
    k1->right = leftLeftRotation(k1->right);

    return rightRightRotation(k1);
}

插入

插入节点的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/* 
 * 将结点插入到AVL树中，并返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::insert(AVLTreeNode<T>* &tree, T key)
{
    if (tree == NULL) 
    {
        // 新建节点
        tree = new AVLTreeNode<T>(key, NULL, NULL);
        if (tree==NULL)
        {
            cout << "ERROR: create avltree node failed!" << endl;
            return NULL;
        }
    }
    else if (key < tree->key) // 应该将key插入到"tree的左子树"的情况
    {
        tree->left = insert(tree->left, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->left) - height(tree->right) == 2)
        {
            if (key < tree->left->key)
                tree = leftLeftRotation(tree);
            else
                tree = leftRightRotation(tree);
        }
    }
    else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
    {
        tree->right = insert(tree->right, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->right) - height(tree->left) == 2)
        {
            if (key > tree->right->key)
                tree = rightRightRotation(tree);
            else
                tree = rightLeftRotation(tree);
        }
    }
    else //key == tree->key)
    {
        cout << "添加失败：不允许添加相同的节点！" << endl;
    }

    tree->height = max( height(tree->left), height(tree->right)) + 1;

    return tree;
}

template <class T>
void AVLTree<T>::insert(T key) {
    insert(mRoot, key);
}

删除

删除节点的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
/* 
 * 删除结点(z)，返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     z 待删除的结点
 * 返回值：
 *     根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::remove(AVLTreeNode<T>* &tree, AVLTreeNode<T>* z) {
    // 根为空 或者 没有要删除的节点，直接返回NULL。
    if (tree==NULL || z==NULL)
        return NULL;

    if (z->key < tree->key)        // 待删除的节点在"tree的左子树"中
    {
        tree->left = remove(tree->left, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->right) - height(tree->left) == 2)
        {
            AVLTreeNode<T> *r =  tree->right;
            if (height(r->left) > height(r->right))
                tree = rightLeftRotation(tree);
            else
                tree = rightRightRotation(tree);
        }
    }
    else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
    {
        tree->right = remove(tree->right, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->left) - height(tree->right) == 2)
        {
            AVLTreeNode<T> *l =  tree->left;
            if (height(l->right) > height(l->left))
                tree = leftRightRotation(tree);
            else
                tree = leftLeftRotation(tree);
        }
    }
    else    // tree是对应要删除的节点。
    {
        // tree的左右孩子都非空
        if ((tree->left!=NULL) && (tree->right!=NULL))
        {
            if (height(tree->left) > height(tree->right))
            {
                // 如果tree的左子树比右子树高；
                // 则(01)找出tree的左子树中的最大节点
                //   (02)将该最大节点的值赋值给tree。
                //   (03)删除该最大节点。
                // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                AVLTreeNode<T>* max = maximum(tree->left);
                tree->key = max->key;
                tree->left = remove(tree->left, max);
            }
            else
            {
                // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                // 则(01)找出tree的右子树中的最小节点
                //   (02)将该最小节点的值赋值给tree。
                //   (03)删除该最小节点。
                // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                AVLTreeNode<T>* min = maximum(tree->right);
                tree->key = min->key;
                tree->right = remove(tree->right, min);
            }
        }
        else
        {
            AVLTreeNode<T>* tmp = tree;
            tree = (tree->left!=NULL) ? tree->left : tree->right;
            delete tmp;
        }
    }

    return tree;
}

template <class T>
void AVLTree<T>::remove(T key) {
    AVLTreeNode<T>* z; 

    if ((z = search(mRoot, key)) != NULL)
        mRoot = remove(mRoot, z);
}

注意：关于AVL树的"前序遍历"、“中序遍历”、“后序遍历”、“最大值”、“最小值”、“查找”、“打印”、"销毁"等接口与"二叉查找树"基本一样，这些操作在"二叉查找树"中已经介绍过了，这里就不再单独介绍了。当然，后文给出的AVL树的完整源码中，有给出这些API的实现代码。

AVL树的C++实现（完整源码）

AVL树的C++实现文件(AVRTree.h)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
#ifndef _AVL_TREE_HPP_
#define _AVL_TREE_HPP_

#include <iomanip>
#include <iostream>
using namespace std;

template <class T>
class AVLTreeNode{
    public:
        T key;                // 关键字(键值)
        int height;         // 高度
        AVLTreeNode *left;    // 左孩子
        AVLTreeNode *right;    // 右孩子

        AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
            key(value), height(0),left(l),right(r) {}
};

template <class T>
class AVLTree {
    private:
        AVLTreeNode<T> *mRoot;    // 根结点

    public:
        AVLTree();
        ~AVLTree();

        // 获取树的高度
        int height();
        // 获取树的高度
        int max(int a, int b);

        // 前序遍历"AVL树"
        void preOrder();
        // 中序遍历"AVL树"
        void inOrder();
        // 后序遍历"AVL树"
        void postOrder();

        // (递归实现)查找"AVL树"中键值为key的节点
        AVLTreeNode<T>* search(T key);
        // (非递归实现)查找"AVL树"中键值为key的节点
        AVLTreeNode<T>* iterativeSearch(T key);

        // 查找最小结点：返回最小结点的键值。
        T minimum();
        // 查找最大结点：返回最大结点的键值。
        T maximum();

        // 将结点(key为节点键值)插入到AVL树中
        void insert(T key);

        // 删除结点(key为节点键值)
        void remove(T key);

        // 销毁AVL树
        void destroy();

        // 打印AVL树
        void print();
    private:
        // 获取树的高度
        int height(AVLTreeNode<T>* tree) ;

        // 前序遍历"AVL树"
        void preOrder(AVLTreeNode<T>* tree) const;
        // 中序遍历"AVL树"
        void inOrder(AVLTreeNode<T>* tree) const;
        // 后序遍历"AVL树"
        void postOrder(AVLTreeNode<T>* tree) const;

        // (递归实现)查找"AVL树x"中键值为key的节点
        AVLTreeNode<T>* search(AVLTreeNode<T>* x, T key) const;
        // (非递归实现)查找"AVL树x"中键值为key的节点
        AVLTreeNode<T>* iterativeSearch(AVLTreeNode<T>* x, T key) const;

        // 查找最小结点：返回tree为根结点的AVL树的最小结点。
        AVLTreeNode<T>* minimum(AVLTreeNode<T>* tree);
        // 查找最大结点：返回tree为根结点的AVL树的最大结点。
        AVLTreeNode<T>* maximum(AVLTreeNode<T>* tree);

        // LL：左左对应的情况(左单旋转)。
        AVLTreeNode<T>* leftLeftRotation(AVLTreeNode<T>* k2);

        // RR：右右对应的情况(右单旋转)。
        AVLTreeNode<T>* rightRightRotation(AVLTreeNode<T>* k1);

        // LR：左右对应的情况(左双旋转)。
        AVLTreeNode<T>* leftRightRotation(AVLTreeNode<T>* k3);

        // RL：右左对应的情况(右双旋转)。
        AVLTreeNode<T>* rightLeftRotation(AVLTreeNode<T>* k1);

        // 将结点(z)插入到AVL树(tree)中
        AVLTreeNode<T>* insert(AVLTreeNode<T>* &tree, T key);

        // 删除AVL树(tree)中的结点(z)，并返回被删除的结点
        AVLTreeNode<T>* remove(AVLTreeNode<T>* &tree, AVLTreeNode<T>* z);

        // 销毁AVL树
        void destroy(AVLTreeNode<T>* &tree);

        // 打印AVL树
        void print(AVLTreeNode<T>* tree, T key, int direction);
};

/*
 * 构造函数
 */
template <class T>
AVLTree<T>::AVLTree():mRoot(NULL)
{
}

/*
 * 析构函数
 */
template <class T>
AVLTree<T>::~AVLTree()
{
    destroy(mRoot);
}

/*
 * 获取树的高度
 */
template <class T>
int AVLTree<T>::height(AVLTreeNode<T>* tree)
{
    if (tree != NULL)
        return tree->height;

    return 0;
}

template <class T>
int AVLTree<T>::height()
{
    return height(mRoot);
}
/*
 * 比较两个值的大小
 */
template <class T>
int AVLTree<T>::max(int a, int b)
{
    return a>b ? a : b;
}

/*
 * 前序遍历"AVL树"
 */
template <class T>
void AVLTree<T>::preOrder(AVLTreeNode<T>* tree) const
{
    if(tree != NULL)
    {
        cout<< tree->key << " " ;
        preOrder(tree->left);
        preOrder(tree->right);
    }
}

template <class T>
void AVLTree<T>::preOrder()
{
    preOrder(mRoot);
}

/*
 * 中序遍历"AVL树"
 */
template <class T>
void AVLTree<T>::inOrder(AVLTreeNode<T>* tree) const
{
    if(tree != NULL)
    {
        inOrder(tree->left);
        cout<< tree->key << " " ;
        inOrder(tree->right);
    }
}

template <class T>
void AVLTree<T>::inOrder()
{
    inOrder(mRoot);
}

/*
 * 后序遍历"AVL树"
 */
template <class T>
void AVLTree<T>::postOrder(AVLTreeNode<T>* tree) const
{
    if(tree != NULL)
    {
        postOrder(tree->left);
        postOrder(tree->right);
        cout<< tree->key << " " ;
    }
}

template <class T>
void AVLTree<T>::postOrder()
{
    postOrder(mRoot);
}

/*
 * (递归实现)查找"AVL树x"中键值为key的节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::search(AVLTreeNode<T>* x, T key) const
{
    if (x==NULL || x->key==key)
        return x;

    if (key < x->key)
        return search(x->left, key);
    else
        return search(x->right, key);
}

template <class T>
AVLTreeNode<T>* AVLTree<T>::search(T key)
{
    return search(mRoot, key);
}

/*
 * (非递归实现)查找"AVL树x"中键值为key的节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::iterativeSearch(AVLTreeNode<T>* x, T key) const
{
    while ((x!=NULL) && (x->key!=key))
    {
        if (key < x->key)
            x = x->left;
        else
            x = x->right;
    }

    return x;
}

template <class T>
AVLTreeNode<T>* AVLTree<T>::iterativeSearch(T key)
{
    return iterativeSearch(mRoot, key);
}

/*
 * 查找最小结点：返回tree为根结点的AVL树的最小结点。
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::minimum(AVLTreeNode<T>* tree)
{
    if (tree == NULL)
        return NULL;

    while(tree->left != NULL)
        tree = tree->left;
    return tree;
}

template <class T>
T AVLTree<T>::minimum()
{
    AVLTreeNode<T> *p = minimum(mRoot);
    if (p != NULL)
        return p->key;

    return (T)NULL;
}

/*
 * 查找最大结点：返回tree为根结点的AVL树的最大结点。
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::maximum(AVLTreeNode<T>* tree)
{
    if (tree == NULL)
        return NULL;

    while(tree->right != NULL)
        tree = tree->right;
    return tree;
}

template <class T>
T AVLTree<T>::maximum()
{
    AVLTreeNode<T> *p = maximum(mRoot);
    if (p != NULL)
        return p->key;

    return (T)NULL;
}

/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::leftLeftRotation(AVLTreeNode<T>* k2)
{
    AVLTreeNode<T>* k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = max( height(k2->left), height(k2->right)) + 1;
    k1->height = max( height(k1->left), k2->height) + 1;

    return k1;
}

/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::rightRightRotation(AVLTreeNode<T>* k1)
{
    AVLTreeNode<T>* k2;

    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = max( height(k1->left), height(k1->right)) + 1;
    k2->height = max( height(k2->right), k1->height) + 1;

    return k2;
}

/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::leftRightRotation(AVLTreeNode<T>* k3)
{
    k3->left = rightRightRotation(k3->left);

    return leftLeftRotation(k3);
}

/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::rightLeftRotation(AVLTreeNode<T>* k1)
{
    k1->right = leftLeftRotation(k1->right);

    return rightRightRotation(k1);
}

/*
 * 将结点插入到AVL树中，并返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::insert(AVLTreeNode<T>* &tree, T key)
{
    if (tree == NULL)
    {
        // 新建节点
        tree = new AVLTreeNode<T>(key, NULL, NULL);
        if (tree==NULL)
        {
            cout << "ERROR: create avltree node failed!" << endl;
            return NULL;
        }
    }
    else if (key < tree->key) // 应该将key插入到"tree的左子树"的情况
    {
        tree->left = insert(tree->left, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->left) - height(tree->right) == 2)
        {
            if (key < tree->left->key)
                tree = leftLeftRotation(tree);
            else
                tree = leftRightRotation(tree);
        }
    }
    else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
    {
        tree->right = insert(tree->right, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->right) - height(tree->left) == 2)
        {
            if (key > tree->right->key)
                tree = rightRightRotation(tree);
            else
                tree = rightLeftRotation(tree);
        }
    }
    else //key == tree->key)
    {
        cout << "添加失败：不允许添加相同的节点！" << endl;
    }

    tree->height = max( height(tree->left), height(tree->right)) + 1;

    return tree;
}

template <class T>
void AVLTree<T>::insert(T key)
{
    insert(mRoot, key);
}

/*
 * 删除结点(z)，返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     z 待删除的结点
 * 返回值：
 *     根节点
 */
template <class T>
AVLTreeNode<T>* AVLTree<T>::remove(AVLTreeNode<T>* &tree, AVLTreeNode<T>* z)
{
    // 根为空 或者 没有要删除的节点，直接返回NULL。
    if (tree==NULL || z==NULL)
        return NULL;

    if (z->key < tree->key)        // 待删除的节点在"tree的左子树"中
    {
        tree->left = remove(tree->left, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->right) - height(tree->left) == 2)
        {
            AVLTreeNode<T> *r =  tree->right;
            if (height(r->left) > height(r->right))
                tree = rightLeftRotation(tree);
            else
                tree = rightRightRotation(tree);
        }
    }
    else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
    {
        tree->right = remove(tree->right, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (height(tree->left) - height(tree->right) == 2)
        {
            AVLTreeNode<T> *l =  tree->left;
            if (height(l->right) > height(l->left))
                tree = leftRightRotation(tree);
            else
                tree = leftLeftRotation(tree);
        }
    }
    else    // tree是对应要删除的节点。
    {
        // tree的左右孩子都非空
        if ((tree->left!=NULL) && (tree->right!=NULL))
        {
            if (height(tree->left) > height(tree->right))
            {
                // 如果tree的左子树比右子树高；
                // 则(01)找出tree的左子树中的最大节点
                //   (02)将该最大节点的值赋值给tree。
                //   (03)删除该最大节点。
                // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                AVLTreeNode<T>* max = maximum(tree->left);
                tree->key = max->key;
                tree->left = remove(tree->left, max);
            }
            else
            {
                // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                // 则(01)找出tree的右子树中的最小节点
                //   (02)将该最小节点的值赋值给tree。
                //   (03)删除该最小节点。
                // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                AVLTreeNode<T>* min = maximum(tree->right);
                tree->key = min->key;
                tree->right = remove(tree->right, min);
            }
        }
        else
        {
            AVLTreeNode<T>* tmp = tree;
            tree = (tree->left!=NULL) ? tree->left : tree->right;
            delete tmp;
        }
    }

    return tree;
}

template <class T>
void AVLTree<T>::remove(T key)
{
    AVLTreeNode<T>* z;

    if ((z = search(mRoot, key)) != NULL)
        mRoot = remove(mRoot, z);
}

/*
 * 销毁AVL树
 */
template <class T>
void AVLTree<T>::destroy(AVLTreeNode<T>* &tree)
{
    if (tree==NULL)
        return ;

    if (tree->left != NULL)
        destroy(tree->left);
    if (tree->right != NULL)
        destroy(tree->right);

    delete tree;
}

template <class T>
void AVLTree<T>::destroy()
{
    destroy(mRoot);
}

/*
 * 打印"二叉查找树"
 *
 * key        -- 节点的键值
 * direction  --  0，表示该节点是根节点;
 *               -1，表示该节点是它的父结点的左孩子;
 *                1，表示该节点是它的父结点的右孩子。
 */
template <class T>
void AVLTree<T>::print(AVLTreeNode<T>* tree, T key, int direction)
{
    if(tree != NULL)
    {
        if(direction==0)    // tree是根节点
            cout << setw(2) << tree->key << " is root" << endl;
        else                // tree是分支节点
            cout << setw(2) << tree->key << " is " << setw(2) << key << "'s "  << setw(12) << (direction==1?"right child" : "left child") << endl;

        print(tree->left, tree->key, -1);
        print(tree->right,tree->key,  1);
    }
}

template <class T>
void AVLTree<T>::print()
{
    if (mRoot != NULL)
        print(mRoot, mRoot->key, 0);
}
#endif

AVL树的C++测试程序

AVL树的测试程序(AVLTreeTest.cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * C 语言: AVL树
 *
 * @author skywang
 * @date 2013/11/07
 */

#include <iostream>
#include "AVLTree.h"
using namespace std;

static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
#define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) )

int main()
{
    int i,ilen;
    AVLTree<int>* tree=new AVLTree<int>();

    cout << "== 依次添加: ";
    ilen = TBL_SIZE(arr);
    for(i=0; i<ilen; i++)
    {
        cout << arr[i] <<" ";
        tree->insert(arr[i]);
    }

    cout << "\n== 前序遍历: ";
    tree->preOrder();

    cout << "\n== 中序遍历: ";
    tree->inOrder();

    cout << "\n== 后序遍历: ";
    tree->postOrder();
    cout << endl;

    cout << "== 高度: " << tree->height() << endl;
    cout << "== 最小值: " << tree->minimum() << endl;
    cout << "== 最大值: " << tree->maximum() << endl;
    cout << "== 树的详细信息: " << endl;
    tree->print();

    i = 8;
    cout << "\n== 删除根节点: " << i;
    tree->remove(i);

    cout << "\n== 高度: " << tree->height() ;
    cout << "\n== 中序遍历: " ;
    tree->inOrder();
    cout << "\n== 树的详细信息: " << endl;
    tree->print();

    // 销毁二叉树
    tree->destroy();

    return 0;
}

在测试程序中，首先新建一棵AVL树，然后依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中；添加完毕之后，再将8从AVL树中删除。AVL树的添加和删除过程如下图：

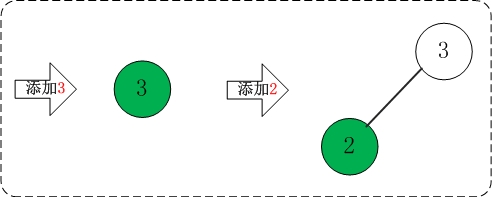
（1）添加3，2

添加3,2都不会破坏AVL树的平衡性。

AVL树添加.jpg

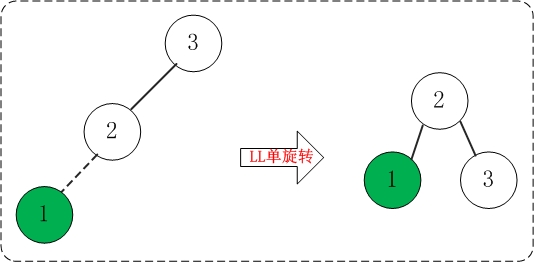
（2）添加1

添加1之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

AVL树添加1.jpg

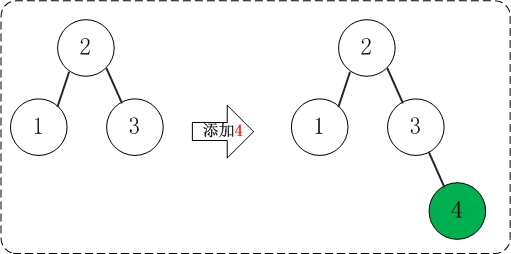
（3）添加4

添加4不会破坏AVL树的平衡性。

AVL树添加4.jpg

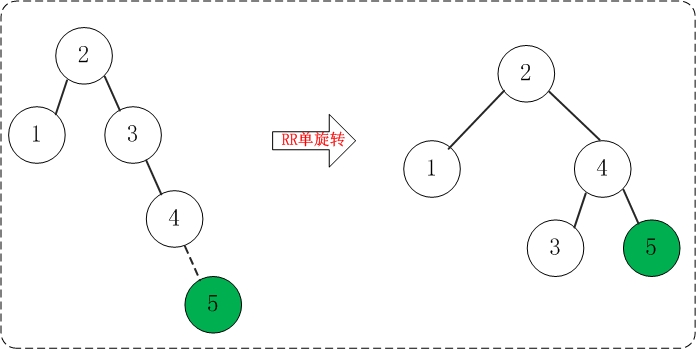
（4）添加5

添加5之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

AVL树添加5.jpg

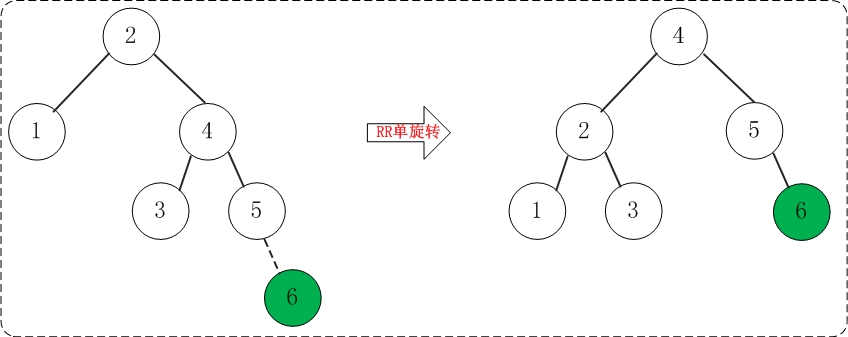
（5）添加6

添加6之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

AVL树添加6.jpg

（6）添加7

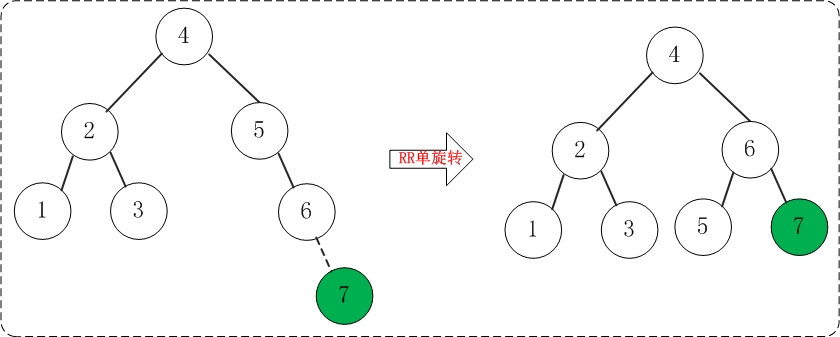
添加7之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

AVL树添加7.jpg

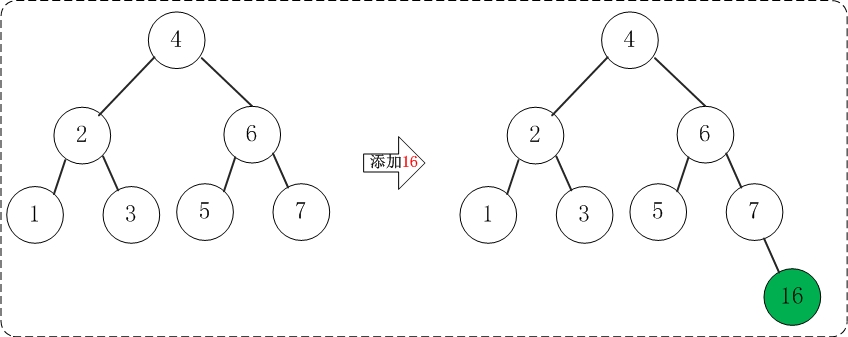
（7）添加16

添加16不会破坏AVL树的平衡性。

AVL树添加16.jpg

（8）添加15

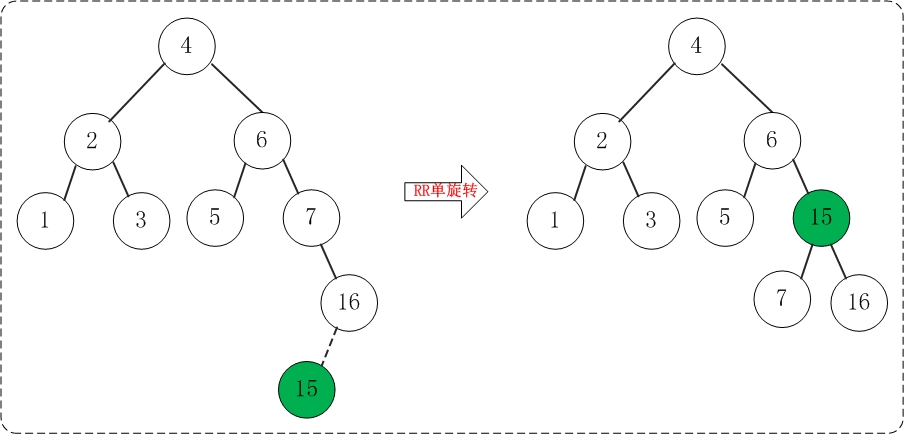
添加15之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

AVL树添加15.jpg

（9）添加14

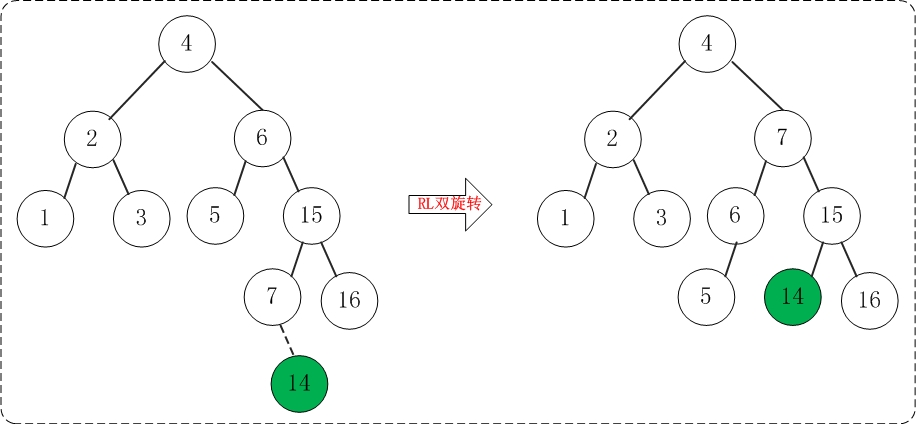
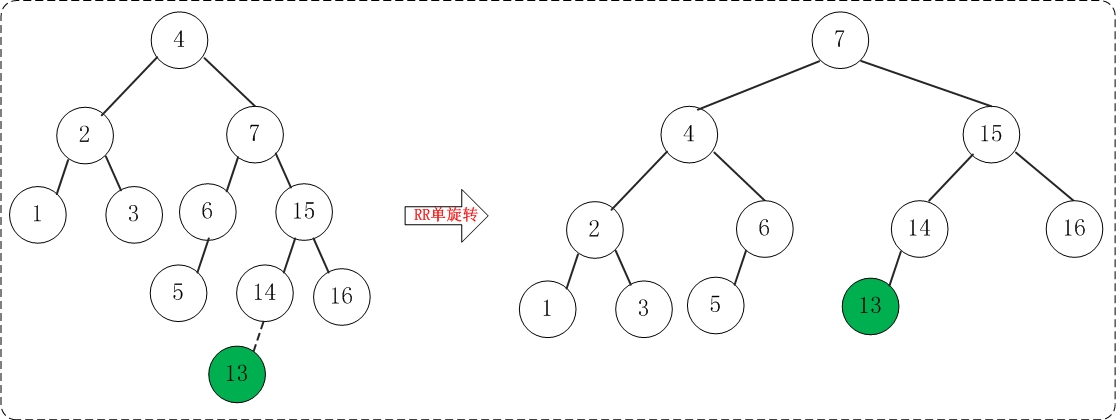
添加14之后，AVL树失去平衡(RL)，此时需要对AVL树进行旋转(RL旋转)。旋转过程如下：

添加14.jpg

（10）添加13

添加13之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

添加13.jpg

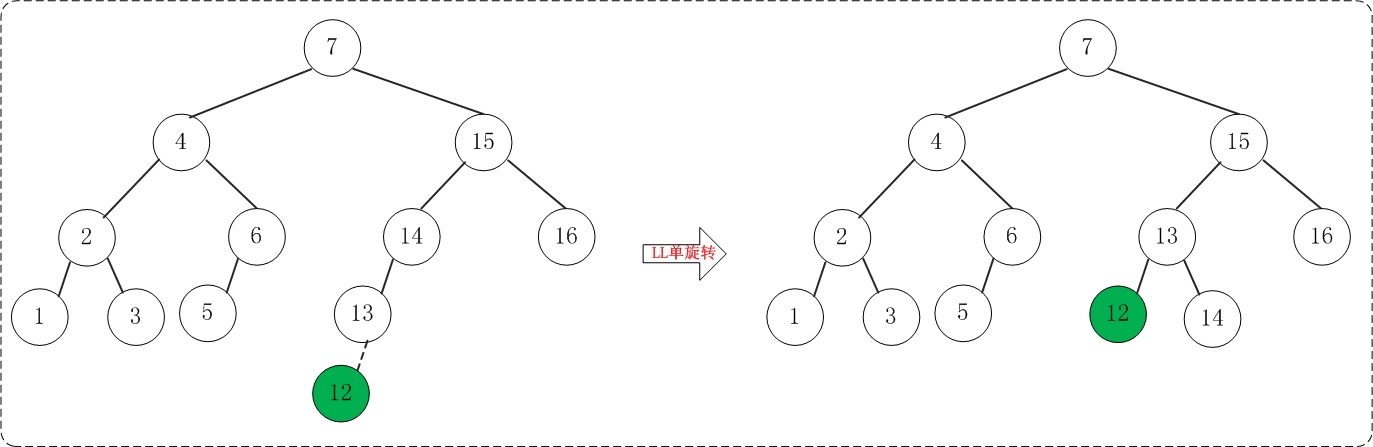
（11）添加12

添加12之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

添加12.jpg

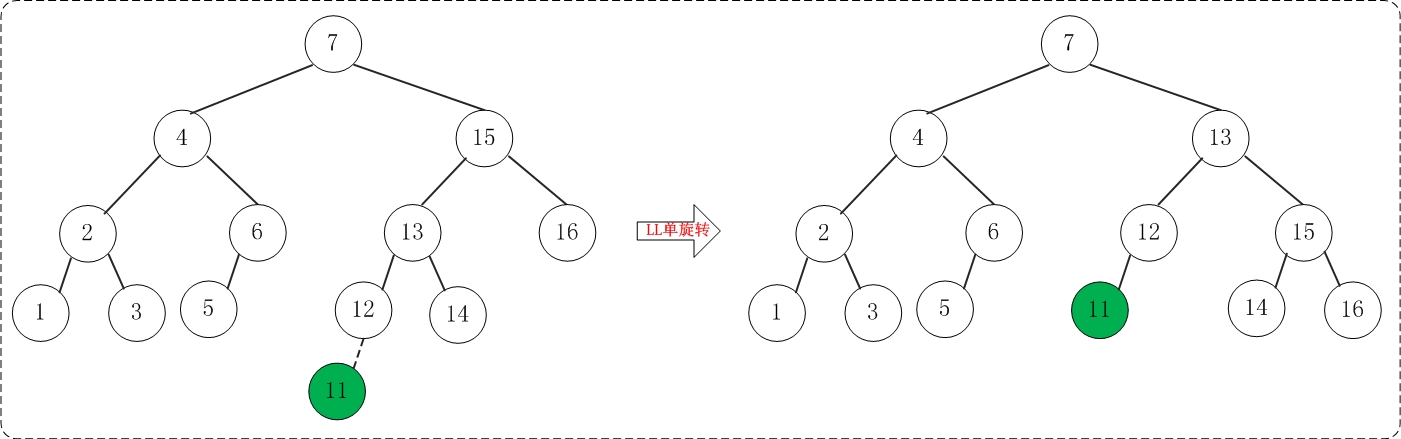
（12）添加11

添加11之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

添加11.jpg

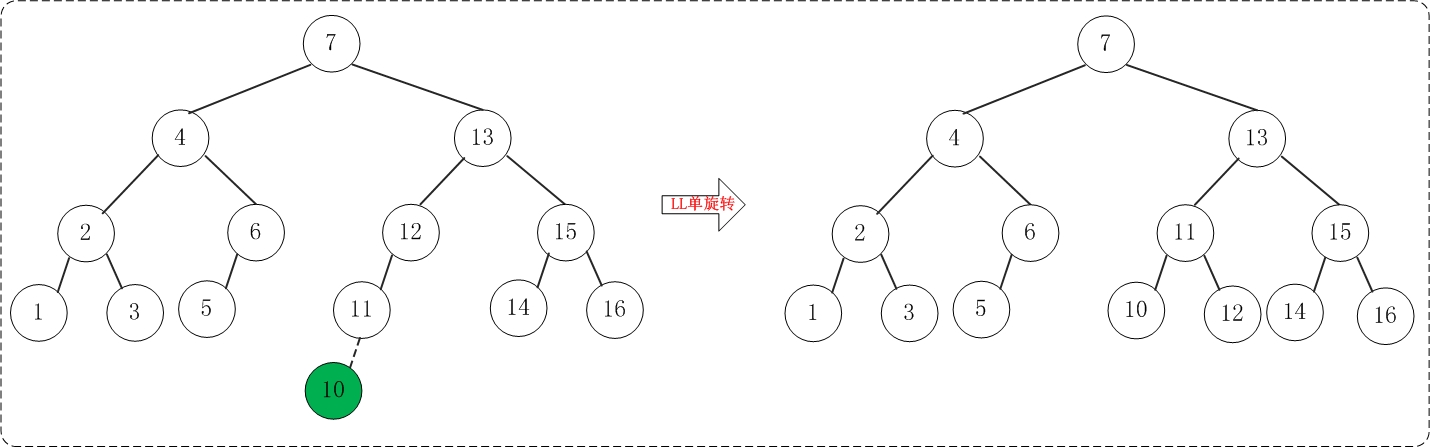
（13）添加10

添加10之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

添加10.jpg

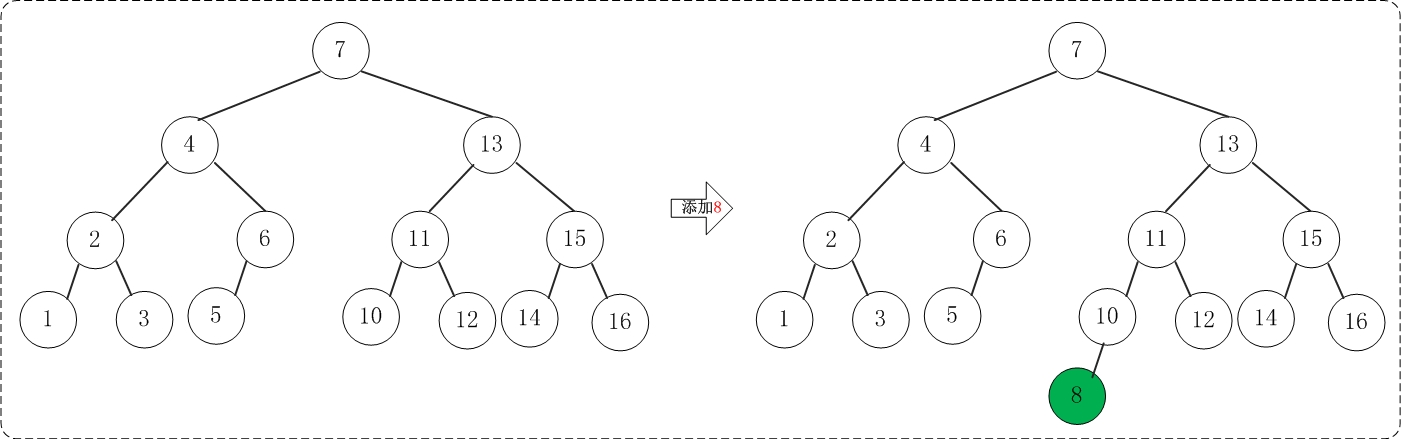
（14）添加8

添加8不会破坏AVL树的平衡性。

添加8.jpg

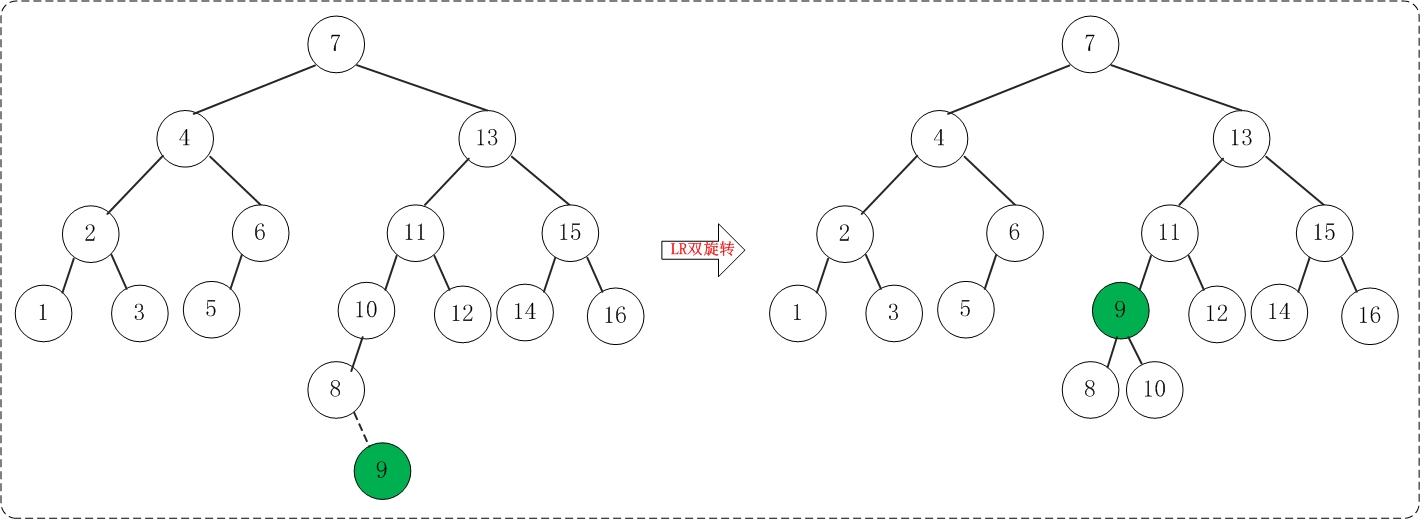
（15）添加9

但是添加9之后，AVL树失去平衡(LR)，此时需要对AVL树进行旋转(LR旋转)。旋转过程如下：

添加9.jpg

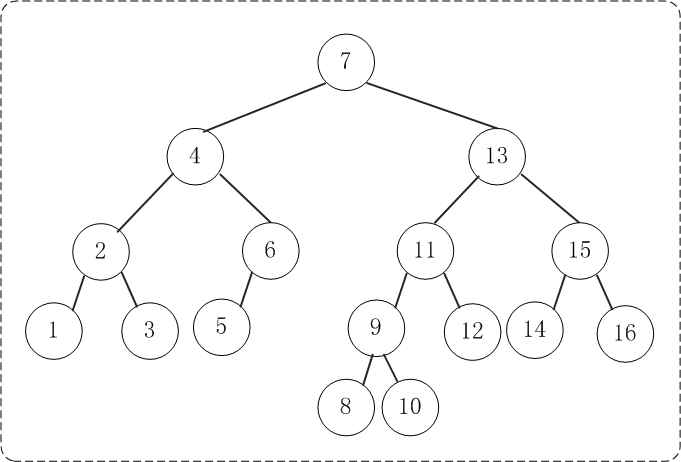
添加完所有数据之后，得到的AVL树如下：

添加完成.jpg

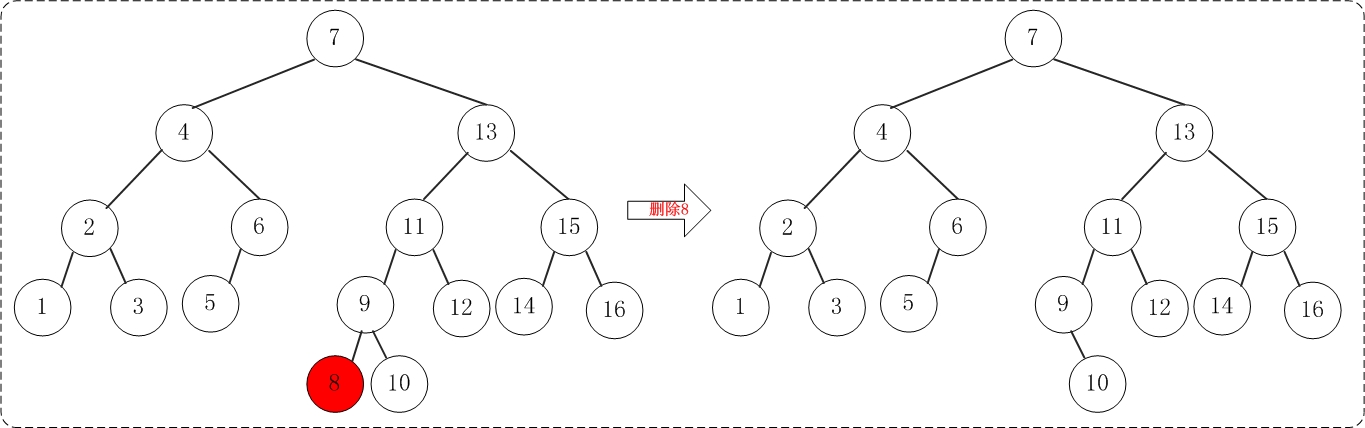
接着，删除节点8.删除节点8并不会造成AVL树的不平衡，所以不需要旋转，操作示意图如下：

删除8.jpg

程序运行结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9 
== 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 
== 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 
== 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7 
== 高度: 5
== 最小值: 1
== 最大值: 16
== 树的详细信息: 
is root
is  7's   left child
is  4's   left child
is  2's   left child
is  2's  right child
is  4's  right child
is  6's   left child
is  7's  right child
is 13's   left child
is 11's   left child
is  9's   left child
is  9's  right child
is 11's  right child
is 13's  right child
is 15's   left child
is 15's  right child

== 删除根节点: 8
== 高度: 5
== 中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 
== 树的详细信息: 
is root
is  7's   left child
is  4's   left child
is  2's   left child
is  2's  right child
is  4's  right child
is  6's   left child
is  7's  right child
is 13's   left child
is 11's   left child
is  9's  right child
is 11's  right child
is 13's  right child
is 15's   left child
is 15's  right child

总结

对AVL树的理论知识进行简单介绍，给出C++实现，并对实现代码进行了测试。

本文转载自：https://www.cnblogs.com/skywang12345/p/3577360.html