欢迎来到我的主页!
0%

LeetCode第一四一题：环形链表

发表于 更新于 分类于
本文字数： 1.3k 阅读时长 ≈ 1 分钟

引言：本文主要介绍leetcode第一四一题，判断一个链表是否有环，并给出其实现。

题目

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

示例

示例1

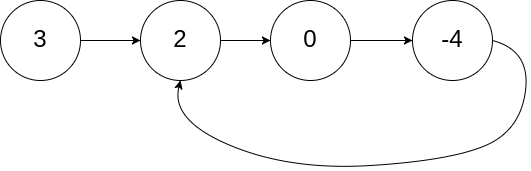
image.png

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例2

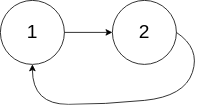
image.png

1
2
3
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例3

image.png

1
2
3
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

  • 链表中节点的数目范围是 [0, 10^4]
  • 10^5 <= Node.val <= 10^5
  • pos 为 -1 或者链表中的一个 有效索引 。

分析

本题目最容易想到的是遍历链表，在遍历的过程中把每个结点存储起来，同时查询存储的里面是否有当前结点，如果有，那么说明是个环，如果遍历完没有，说明没有环；但是链表判圈有更加适合的判圈算法——佛洛依德判圈算法。

实现

实现一（哈希）

1
2
3
4
5
6
7
8
9
10
11
bool hasCycle(ListNode *head) {
    unordered_set<ListNode*> hashset;
    while (head != nullptr) {
        if (hashset.find(head) != hashset.end()) {
            return true;
        }
        hashset.emplace(head);
        head = head->next;
    }
    return false;
}

时间复杂度：O(n)

空间复杂度：O(n)

实现二（判圈算法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool hasCycle(ListNode *head) {
    ListNode *slow = new ListNode(0);
    slow->next = head;
    ListNode *fast = new ListNode(0);
    fast->next = head;
    while (fast != nullptr && fast->next != nullptr) {
        if (fast == slow) {
            return true;
        }
        fast = fast->next->next;
        slow = slow->next;
    }
    return false;
}

时间复杂度：O(n)

空间复杂度：O(1)

注意开始的状态，要把slow和fast定义为不同的指针，否则直接就输出true了，总而言之，一定要保证特殊情况下，尤其是开始状态的正确性

拓展

1.哈希容器（无序关联式容器）

2.佛洛依德判圈算法